Data Science
Multi-disciplinary field that brings together concepts from computer science, statistics/machine learning, and data analysis to understand and extract insights from the ever-increasing amounts of data.
-
Hypothesis-Driven: Given a problem, what kind of data do we need to help solve it?
-
Data-Driven: Given some data, what interesting problems can be solved with it
-
what can we learn from data and what actions to take?
Types of data
-
Structured: Data that has predefined structures. e.g. tables, spreadsheets, or relational databases.
-
Unstructured Data:: Data with no predefined structure, comes in any size or form, CANNOT be easily stored in tables. e.g. blobs of text, images, audio
-
Quantitative Data: Numerical. e.g. height, weight
-
Categorical Data: Data that can be labeled or divided into groups. e.g. race, sex, hair color.
-
Big Data: Massive datasets, or data that contains; greater variety arriving in increasing volumes and with ever-higher velocity (3 Vs). Cannot fit in the memory of a single machine.
Data Source / Format
Most Common Data Formats
CSV, XML, SQL, JSON, Protocol Bu↵ers
Data Sources
Companies/Proprietary Data, APIs, Gov- ernment, Academic, Web Scraping/Crawling
Data Science Problem Types:
Classification:
Assigning something to a discrete set of possibilities. e.g. spam or non-spam, Democrat or Repub- lican, blood type (A, B, AB, O)
Regression:
Predicting a numerical value. e.g. some- one’s income, next year GDP, stock price
Probablity
Probability theory provides a framework for reasoning about likelihood of events.
Experiment:
procedure that yields one of a possible set of outcomes e.g. repeatedly tossing a die or coin.
Sample Space S:
set of possible outcomes of an experi- ment e.g. if tossing a die, S = (1,2,3,4,5,6)
Event E:
set of outcomes of an experiment e.g. event thatarollis5,ortheeventthatsumof2rollsis7
Probability of an Outcome
s or P(s): number that satisfies 2 properties.
\[0\leq P(s) \leq 1\] \[\sum P(s) = 1\]Probability of Event E:
sum of the probabilities of the outcomes of the experiment: \(p(E) = \sum Ps⇢E p(s)\)
Random Variable V:
numerical function on the out- comes of a probability space
Expected Value V:
\(E(V) = \sum(s\space belongs\space to\space s) P(s) * V(s)\)
Indepedence Conditional Compound

Probability Distributions
Probability Density Function (PDF):
Gives the prob- ability that a rv takes on the value x: pX(x) = P(X = x)
Cumulative Density Function (CDF)
Gives the prob- ability that a random variable is less than or equal to x: FX(x)=P(Xx)
Note: The PDF and the CDF of a given random variable contain exactly the same information.
Descriptive Stats:
Centrality:
Central limit Theorem:
In probability theory, the central limit theorem establishes that, in some situations, when independent random variables are added, their properly normalized sum tends toward a normal distribution even if the original variables themselves are not normally distributed
Arithematic Mean:
best when character symmetric distribution without outliers: 1/n sigma X
Geometric Mean:
Always smaller than arithematic means: useful to capture averaging ratios mean = Nth root of a1 a2 …a3
\(^n\sqrt{a_{1}*a_{2}* ... * a_{n}}\)
median
mode:
most frequent value
variabiliy:
- standard deviation: Measure the square difference between the elements and mean 看每个直的平方和平均值差多少 REMEMBER TO /(N-1) GIVEN LARGE N FOR DEGREE OF FREEDOM
- Variance V = SIGMA SQAURE 2
variance interpret:
Variance is an inherent part of the universe. It is impossible to obtain the same results after repeated observations of the same event due to random noise/error. Variance can be explained away by attributing to sampling or measurement errors. Other times, the variance is due to the random fluctuations of the universe.
Correlation Analysis:
Correlation coefficients r(X,Y) is a statistic that measures the degree that Y is a function of X and vice versa. Correlation values range from -1 to 1, where 1 means fully correlated, -1 means negatively-correlated, and 0 means no correlation.
Person Coeffcicent:
- Measures the degree of the relationship between linear related variables: R
Spearman Rank Coefficient:
- Computed on ranks and depicts monotonic ????? relationship
Check out more about Spearman’s Rank Correlation Coefficient
- A correlation can easily be drawn as a scatter graph, but the most precise way to compare several pairs of data is to use a statistical test - this establishes whether the correlation is really significant or if it could have been the result of chance alone.
- Spearman’s Rank correlation coefficient is a technique which can be used to summarise the strength and direction (negative or positive) of a relationship between two variables.
Note: Correlation does not imply causation

Data Cleaning
Data Cleaning is the process of turning raw data into a clean and analyzable data set. ”Garbage in, garbage out.” Make sure garbage doesn’t get put in.
Missing Data
Missing Data Influene:
- shrink the sample size
- precision of confidence intervals is harmed
- statistical power weakens
- parameter estimates may be biased
Missing data mechanisms
Missing completely at random (MCAR):
- Suppose variable Y has some missing values. We will say that these values are MCAR if the probability of missing data on Y is unrelated to the value of Y itself or to the values of any other variable in the data set. However, it does allow for the possibility that “missingness” on Y is related to the “missingness” on some other variable X. (Briggs et al., 2003) (Allison, 2001)
Missing at random (MAR)-a weaker assumption than MCAR
-
The probability of missing data on Y is unrelated to the value of Y after controlling for other variables in the analysis (say X). Formally: P(Y missing Y,X) = P(Y missing X) (Allison, 2001).
Not missing at random (NMAR):
- Missing values do depend on unobserved values.
Example:
The NMAR assumption would be fulfilled if people with high income are less likely to report their income.
NOTE
If MAR assumption is not fulfilled: The missing data mechanism is said to be nonignorable and, thus, it must be modeled to get good estimates of the parameters of interest. This requires a very good understanding of the missing data process
Errors vs. Artifacts
-
Errors: information that is lost during acquisition and can never be recovered e.g. power outage, crashed servers.
-
Artifacts: systematic problems that arise from the data cleaning process. these problems can be corrected but we must first discover them
Methods for handling missing data
Conventional methods:
- Listwise deletion (or complete case analysis): If a case has missing data for any of the variables, then simply exclude that case from the analysis. It is usually the default in statistical packages. (Briggs et al.,2003).
Advantages: It can be used with any kind of statistical analysis and no special computational methods are required.
Limitations: It can exclude a large fraction of the original sample.
- Data Imputation Process of dealing with missing values.
- The proper meth- ods depend on the type of data we are working with. Gen- eral methods include:
- Drop all records containing missing data
- Heuristic-Based: make a reasonable guess based on knowledge of the underlying domain
- Mean Value: fill in missing data with the mean
- Random Value
- Nearest Neighbor: fill in missing data using similar
- Interpolation: use a method like lin
- Marginal mean imputation:ComputethemeanofXusingthenon-missingvaluesanduseitto impute missing values of X.
- Conditional Mean Imputation:
If the data are MCAR, least-squares coefficients are consistent (i.e. unbiased as the sample size increases) but they are not fully efficient (remember, efficiency is a measure of the optimality of an estimator. Essentially, a more efficient estimator, experiment or test needs fewer samples than a less efficient one to achieve a given performance). Estimating the model using weighted least squares or generalized least squares leads to better results (Graham, 2009) (Allison, 2001) and (Briggs et al., 2003).
Limitations of imputation techniques in general
They lead to an underestimation of standard errors and, thus, overestimation of test statistics. The main reason is that the imputed values are completely determined by a model applied to the observed data, in other words, they contain no error (Allison, 2001).
Advanced Methods
- Multiple Imputation : The imputed values are draws from a distribution, so they inherently contain some variation. Thus, multiple imputation (MI) solves the limitations of single imputation by introducing an additional form of error based on variation in the parameter estimates across the imputation, which is called “between imputation error”. It replaces each missing item with two or more acceptable values, representing a distribution of possibilities (Allison, 2001).
MI is a simulation-based procedure
- Maximum Likelihood We can use this method to get the variance-covariance matrix for the variables in the model based on all the available data points, and then use the obtained variance- covariance matrix to estimate our regression model (Schafer, 1997).
Compared to MI, MI requires many more decisions than ML (whether to use Markov Chain Monte Carlo (MCMC) method or the Fully Conditional Specification (FCS), how many data sets to produce, how many iterations between data sets, what prior distribution to use-the default is Jeffreys-, etc.). On the other hand, ML is simpler as you only need to specify your model of interest and indicate that you want to use ML ( SAS Institute, 2005).
Direct Maximum Likelihood:
It implies the direct maximization of the multivariate normal likelihood function for the assumed linear model. Advantage: It gives efficient estimates with correct standard errors. Limitations: It requires specialized software (it may be challenging and time consuming).
The Expectation-maximization (EM) algorithm:
It provides estimates of the means and covariance matrix, which can be used to get consistent estimates of the parameters of interest. It is based on an expectation step and a maximization step, which are repeated several times until maximum likelihood estimates are obtained. It requires a large sample size and that the data are missing at random (MAR). Advantage: We can use SAS, since this is the default algorithm it employs for dealing with missing data with Maximum Likelihood. Limitations: Only can be used for linear and log-linear models
Other advanced methods
Bayesian Simulation Method:
- Schafer algorithms: It uses Bayesian iterative simulation methods to impute data sets assuming MAR. Precisely, it splits the multivariate missing problem into a series of univariate problems based on the assumed distribution of the multivariate missing variables (e.g. multivariate normal for continuous variables, multinomial loglinear for categorical variables). In other words, it uses an iterative algorithm that draws samples from a sequence of univariate regressions.
Univariate Regression
-
Van Buuren algorithm : It is a semi-parametric approach. The parametric part implies that each variable has a separate imputation model with a set of predictors that explain the missingness. The non-parametric part implies the specification of an appropriate form (e.g. linear), which depends on the kind of variables.
-
Hot-deck imputation: This method completes a missing observation by selecting at random, with replacement, a value from those individuals who have matching observed values for other variables. In other words, a missing value is imputed based on an observed value that is closer in terms of distance.
Outlier Detection:
- usually arised from data collecting
- use sanity check to solve the problem
Miscellaneous
Lowercasing, removing non-alphanumeric, repairing, unidecode, removing unknown characters
Notes:
- ALways use the raw data to clean, don;t start from a precleaned data.
- always remember to reserve the raw data intact to keep the original accuracy
- Any type of data cleaning/analysis should be done on a copy of the raw data.
Check out more about missing data
Feature Engineering:
Feature engineering is the process of using domain knowl- edge to create features or input variables that help ma- chine learning algorithms perform better. Done correctly, it can help increase the predictive power of your models. Feature engineering is more of an art than science. FE is one of the most important steps in creating a good model.
Continuous Data
- Raw Measures: data that hasn’t been transformed yet
- Rounding: sometimes precision is noise; round to nearest integer, decimal etc..
- Scaling: log, z-score, minmax scale
- Binning: transforming numeric features into categorical ones (or binned) e.g. values between 1-10 belong to A, between 10-20 belong to B, etc.
- Sampling From Distributions
- Interactions: interactions between features: e.g. sub- traction, addition,multiplication, statistical test
- Statistical: log/power transform (helps turn skewed distributions more normal), Box-Cox
- Row Statistics: number of NaN’s, 0’s, negative values, max, min, etc
- Dimensionality Reduction: using PCA, clustering, factor analysis etc
Discrete Data
- Encoding: since some ML algorithms cannot work on categorical data, we need to turn categorical data into nu- merical data or vectors
- Ordinal Values: convert each distinct features into a random number (e.g. [r,g,b] becomes [1,2,3])
- One-Hot Encoding: each of the m features becomes a vector of length m with containing only one 1 (e.g. [r, g, b] becomes [[1,0,0],[0,1,0],[0,0,1]])
- Feature Hashing Scheme: turns arbitrary features into indices in a vector or matrix
- Embeddings: if using words, convert words to vectors (word embeddings)
Statistical Analysis
Process of statistical reasoning: there is an underlying population of possible things we can potentially observe and only a small subset of them are actually sampled (ide- ally at random). Probability theory describes what prop- erties our sample should have given the properties of the population, but statistical inference allows us to deduce what the full population is like after analyzing the sample.

Sampling From Distributions
Inverse Transform Sampling
- Sampling points from a given probability distribution is sometimes necessary to run simulations or whether your data fits a particular distribution. The general technique is called inverse transform sampling or Smirnov transform. First draw a random number p between [0,1]. Compute value x such that the CDF equals p: FX(x) = p. Use x as the value to be the random value drawn from the distribution described by FX (x).
Monte Carlo Sampling
- In higher dimensions, correctly sampling from a given distribution becomes more tricky. Generally want to use Monte Carlo methods, which typically follow these rules: define a domain of possible inputs, generate random inputs from a probability distribution over the domain, perform a deterministic calculation, and analyze the results.
Distributions:
Binomial
Normal/ Gaussian
Poisson (over time)
Power Law Distribution:
The power law (also called the scaling law) states that a relative change in one quantity results in a proportional relative change in another

Modeling-Overview
Modeling
- is the process of incorporating information into a tool which can forecast and make predictions. Usually, we are dealing with statistical modeling where we want to analyze relationships between variables. Formally, we want to estimate a function f (X ) such that:
Statistical learning
- is set of approaches for estimating this f (X ).
Prediction:
once we have a good estimate f(X), we can use it to make predictions on new data. We treat fˆ as a black box, since we only care about the accuracy of the predictions, not why or how it works.
Inference:
we want to understand the relationship between X and Y. We can no longer treat fˆ as a black box since we want to understand how Y changes with respect to X = (X1, X2, …Xp)
More About c
The error term c is composed of the reducible and irreducible error, which will prevent us from ever obtaining a perfect fˆ estimate.
- Reducible: error that can potentially be reduced by using the most appropriate statistical learning technique to estimate f. The goal is to minimize the reducible error. Y =f(X)+c
- Irreducible: error that cannot be reduced no matter how well we estimate f. Irreducible error is unknown and unmeasurable and will always be an upper bound for c.
Variance and Bias tradeoff
There will always be tradeoff between model flexibility (prediction) and model interpretability (inference). This is just another case of the bias-variance trade-off. Typically, as flexibility increases, interpretability decreases. Much of statistical learning/modeling is finding a way to balance the two.
Modeling- Philosophies
Modeling is the process of incorporating information into a tool which can forecast and make predictions.
Designing and validating models is important, as well as evaluating the performance of models. Note that the best forecasting model may not be the most accurate one.
Philosophies of modeling:
Occam’s Razor
Philosophical principle that the simplest explanation is the best explanation. In modeling, if we are given two models that predicts equally well, we should choose the simpler one. Choosing the more complex one can often result in overfitting.
Bias Variance Trade-Off
Inherent part of predictive modeling, where models with lower bias will have higher variance and vice versa. Goal is to achieve low bias and low variance.
Bias:
error from incorrect assumptions to make target function easier to learn (high bias ! missing rel- evant relations or underfitting)
Variance:
error from sensitivity to fluctuations in the dataset, or how much the target estimate would di↵er if different training data was used (high vari- ance ! modeling noise or overfitting)
note: both bias and variance are errors
No Free Lunch Theorem
No single machine learning algorithm is better than all the others on all problems. It is common to try multiple models and find one that works best for a particular problem.
Thinking Like Nate Silve
- Think Probabilistically Probabilistic forecasts are more meaningful than concrete statements and should be reported as probability distributions,.
Incorporate New Information
- Incorporate New Information Use live models, which continually updates using new information. To up-date, use Bayesian reasoning to calculate how probabilities change in response to new evidence.
Consensus Forecast
- Look For Consensus Forecast Use multiple distinct sources of evidence. Some models operate this way, such as boosting and bagging, which uses large number of weak classifiers to produce a strong one.
Modeling- Taxonomy
Parametric vs. Nonparametric
Parametric:
models that first make an assumption about a function form, or shape, of f (linear). Then fits the model. This reduces estimating f to just estimating set of parameters, but if our assumption was wrong, will lead to bad results.
Non-Parametric:
models that don’t make any as- sumptions about f, which allows them to fit a wider range of shapes; but may lead to overfitting
Supervised vs. Unsupervised
Supervised:
models that fit input variables xi = (x1 , x2 , …xn ) to a known output variables yi = (y1, y2, …yn)
Unsupervised:
models that take in input variables xi = (x1, x2, …xn), but they do not have an asso- ciated output to supervise the training. The goal is understand relationships between the variables or observations.
Blackbox vs. Descriptive
Blackbox
models that make decisions, but we do not know what happens ”under the hood” e.g. deep learning, neural networks
Descriptive:
models that provide insight into why they make their decisions e.g. linear regression, de- cision trees
First-Principle vs. Data-Driven
First-Principle:
models based on a prior belief of how the system under investigation works, incorpo- rates domain knowledge (ad-hoc)
Data-Driven:
models based on observed correlations between input and output variables
Deterministic vs. Stochastic
Deterministic:
models that produce a single ”pre- diction” e.g. yes or no, true or false
Stochastic:
models that produce probability distributions over possible events
Flat vs. Hierarchical
Flat:
models that solve problems on a single level, no notion of subproblems
Hierarchical:
models that solve several di↵erent nested subproblems

Modeling- Evaluation Metrics
Need to determine how good our model is. Best way to assess models is out-of-sample predictions (data points your model has never seen).
Classification:
| Predicted Yes | Predicted No | |
|---|---|---|
| Actual Yes | True Positives (TP) | False Negatives (FN) |
| Actual No | False Positives (FP) | True Negatives (TN) |
Accuracy:
Ratio of correct predictions over total predictions. Misleading when class sizes are substantially different.
Accuracy = (TP+TN) / (TP+FN+FP+TN)
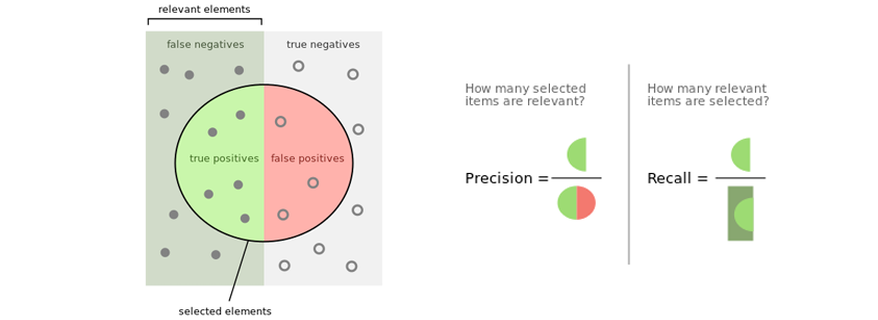
Precision:
How often the classifier is correct when it predicts positive: precision = TP / TP+FP
Fisher exact test
- This test for testing the null of independence of rows and columns in a contingency table with fixed marginals.
- This test uses Chi-squre
- The chi-square uses a procedure that assumes a fairly large sample size. With small sample sizes the chi-square test generates falsely low p-values that exaggerate the significance of findings. Specifically, when the expected number of observations under the null hypothesis in any cell of the 2x2 table is less than 5, the chi-square test exaggerates significance. When this occurs, Fisher’s Exact Test is preferred.
Model Selection
Cross Validation
K-Fold Cross Validation
- One of the most common technique for model evaluation and model selection in machine learning practice is K-fold cross validation. The main idea behind cross-validation is that each observation in our dataset has the opportunity of being tested. K-fold cross-validation is a special case of cross-validation where we iterate over a dataset set k times. In each round, we split the dataset into 𝑘 parts: one part is used for validation, and the remaining 𝑘−1 parts are merged into a training subset for model evaluation. The figure below illustrates the process of 5-fold cross-validation:
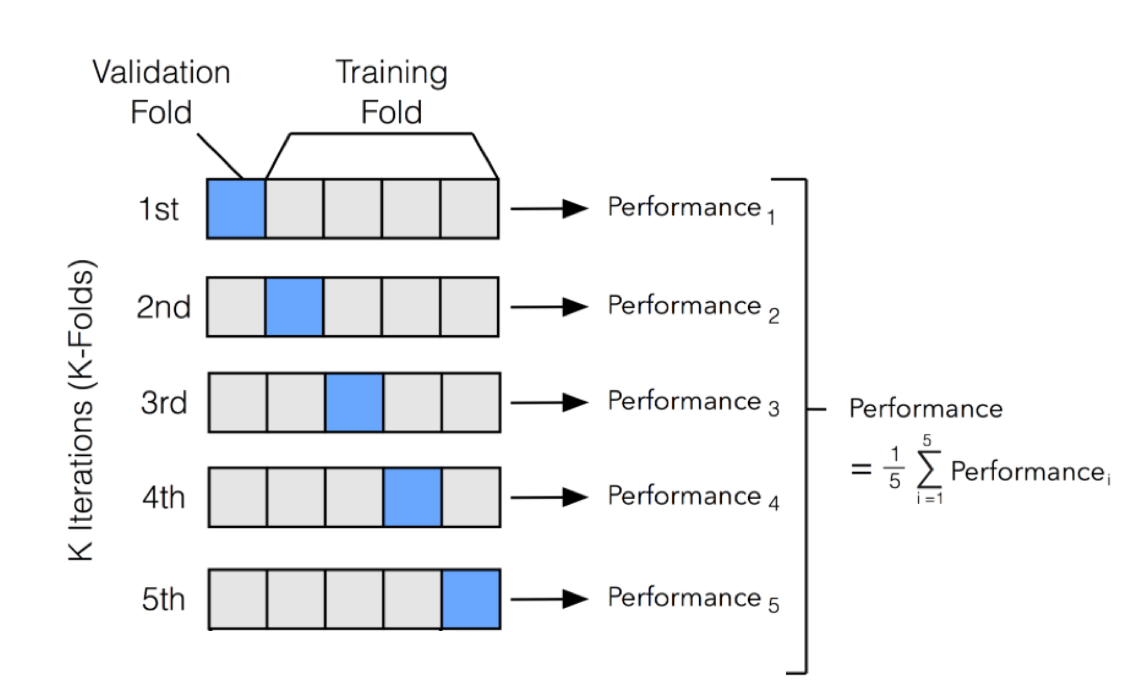
- We use a learning algorithm with fixed hyperparameter settings to fit models to the training folds in each iteration. In 5-fold cross-validation, this procedure will result in 5 models fitted on distinct yet partly overlapping training sets and evaluated on non-overlapping validation sets. Eventually, we compute the cross-validation performance as the arithmetic mean over the 𝑘 performance estimates from the validation sets. The main benefit behind this approach versus a simple train/test split is to reduce the pessimistic bias by using more training data in contrast to setting aside a relatively large portion of the dataset as test data. The following section shows a vanilla implementation of how to generate a K-fold data split.
stats power
- The power of a binary hypothesis test is the probability that the test rejects the null hypothesis when a specific alternative hypothesis is true. The statistical power ranges from 0 to 1, and as statistical power increases, the probability of making a type II error decreases.
Factor Analysis
stats power
Dimension Reduction
Box Cox
One-Hot Encoding
Each of the m features becomes a vector of length m with containing only one 1 (e.g. [r, g, b] becomes [[1,0,0],[0,1,0],[0,0,1]])
Embeddings:
if using words, convert words to vectors (word embeddings)
Cheatsheet PDF
eidted by Michael Miao 12/11/2019
Please download the PDF to view it: Download PDF.</p> </embed> </object>

Recall and Precision
- Precision: among selected how many are correct
- Recall: overall good cases, how many are selected by the model
updating…
edited by Micahel Miao Apri 9th 2022.